Si vous avez lu l’article sur les degrés, vous savez que nous avons mentionné seulement les 7 notes de la musique occidentale (do, ré, mi, fa, sol, la, si). Mais comment référencer les degrés pour les autres notes (do dièse, ré dièse, fa dièse, sol dièse, la dièse) ? Pour cela, une définition plus complète est nécessaire, comme nous allons le voir :
La première note est représentée par le premier degré, ce que nous avons déjà abordé. Ce degré peut aussi être appelé premier degré majeur. Prenons do comme exemple de premier degré.
Dans ce cas, la note ré est le deuxième degré, aussi appelé deuxième degré majeur. La note do dièse (ou ré bémol) est alors le deuxième degré mineur. Les termes « deuxième degré mineur » et « deuxième degré majeur » sont souvent abrégés en « seconde mineure » et « seconde majeure« , et il en va de même pour les autres degrés majeurs et mineurs. Cette nomenclature (majeur et mineur) est utilisée pour indiquer si l’intervalle (la distance entre les notes) est grand ou petit.
Les intervalles majeurs sont grands et les intervalles mineurs sont petits. Dans l’exemple précédent, le « deuxième degré majeur » représentait un intervalle d’un ton entier (car ré est à deux demi-tons au-dessus de do), et le « deuxième degré mineur » un intervalle d’un demi-ton (do dièse est à un demi-ton au-dessus de do). Ces appellations servent à indiquer la distance entre les notes.
En appliquant ce concept à toutes les notes, en partant de C, nous obtenons les suivants :
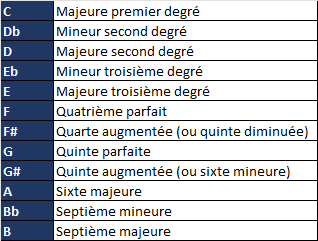
Vous vous demandez peut-être pourquoi il existe les dénominations « augmenté« , « parfait » et « diminué« . Ces termes sont simplement des définitions utilisées dans le langage de la théorie musicale, que vous rencontrerez dans tout livre de théorie musicale ou recueil de chansons.
La logique derrière ces dénominations est similaire à celle des termes « majeur » et « mineur« . « Augmenté » indique un intervalle plus grand, tandis que « diminué » indique un intervalle plus petit. « Parfait » se situe entre ces deux.
Vous pourriez vous demander si nous ne pourrions pas simplement utiliser les termes « majeur » et « mineur » pour toutes les notes, au lieu de « diminué », « augmenté » et « parfait » ? Techniquement, oui, c’est possible. Alors, pourquoi y a-t-il d’autres termes ? Dans des sujets plus avancés, vous verrez que cela est assez utile. Pour le moment, contentez-vous de mémoriser ces nomenclatures et leur signification. Comme vous pouvez le voir, il n’y a pas de mystère, ce sont simplement des termes attribués à des distances spécifiques entre les notes.
Nous allons maintenant appliquer cette nomenclature en partant de notes autres que do (en utilisant uniquement des notes dièses) :
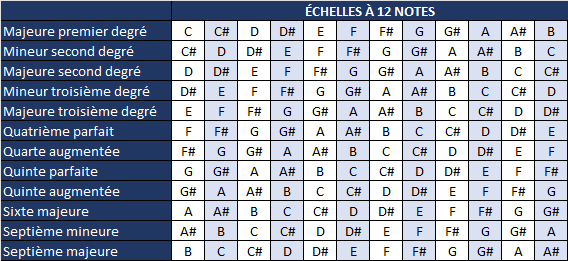
À partir du septième degré, les notes recommencent à se répéter, étant donné que le 8ème degré est identique au 1er degré. Selon cette logique :
- Le 9ème degré est identique au 2ème degré.
- Le 11ème degré est identique au 4ème degré.
- Le 13ème degré est identique au 6ème degré.
Vous vous demandez peut-être : si les degrés au-delà du septième se répètent, pourquoi utiliser les notations 9ème, 11ème et 13ème ?
La raison est que certains musiciens préfèrent ces degrés pour préciser l’octave à utiliser. Par exemple, si un accord est noté Cm6, vous formerez vraisemblablement l’accord de do mineur en y ajoutant le sixième degré le plus proche pour créer Cm6. En revanche, si l’accord est noté Cm13, cela indique que vous devriez utiliser le sixième degré une octave plus haut, et non le sixième degré le plus proche. La seule différence entre ces deux accords est le son, légèrement modifié en fonction de l’octave utilisée pour le 6ème degré (nous approfondirons tout ce que vous devez savoir sur les accords et leurs notations dans les prochains sujets, donc ne vous inquiétez pas si vous ne comprenez pas immédiatement cet exemple).
Pour l’extension de la 9ème, elle est presque toujours jouée une octave plus haut, d’où son usage en lieu et place du 2ème degré. Cependant, il n’est pas rare de voir le numéro 2 utilisé dans les notations d’accords, surtout dans les notations américaines où le numéro 2 est souvent préféré au numéro 9.
Il est important de comprendre ces subtilités pour éviter toute confusion concernant ces nomenclatures.
Maintenant, explorons l’utilité pratique de cette notation !
Application du Concept
Nous pouvons désigner n’importe quelle note en utilisant une note de référence, comme nous l’avons fait dans l’article « Qu’est-ce que les degrés ?« . Nous appliquerons le même principe ici, en complétant simplement le sujet.
Toutefois, précédemment, nous nous sommes concentrés sur la échelle de C majeur. Lorsque nous mentionnions simplement « 3ème degré », « 6ème degré », etc., nous ne spécifiions pas si le degré était majeur, mineur, parfait, diminué ou augmenté. Ainsi, il fallait préciser que les degrés étaient basés sur la structure de la échelle majeure. Maintenant, il ne sera plus nécessaire de se référer à une échelle spécifique, car nous définirons chaque degré individuellement. Voici quelques exemples ci-dessous (comme exercices) :
- Troisième degré mineur de C: E bemol
- Septième degré mineur de G : F
- Deuxième degré mineur de D : E bemol
- Cinquième degré augmenté de C : G dièse
- Quatrième degré parfait (ou quatrième degré) de A : D
- Cinquième degré diminué de B : F
Vous pouvez vérifier ces réponses avec le tableau que nous avons présenté précédemment.
Note : Pour le moment, nous ne discutons que des notes, et non des accords ! Les termes « augmenté » et « diminué », ainsi que « majeur » et « mineur », s’appliquent aussi aux accords, mais c’est une approche différente ! Veillez à ne pas confondre les deux : ici, nous parlons uniquement de notes et de leur nomenclature individuelle. Lorsqu’il s’agit d’accords, la nomenclature a une autre fonction. C’est pourquoi cette distinction est essentielle. Gardez cela à l’esprit.
Poursuivre vers : Octave
Revenir au : Module 2
