En mathématiques et en musique, nous avons exploré ce sujet fascinant pour vous dévoiler les liens étroits entre ces deux domaines. Peut-être que les maths ne vous passionnent pas, mais rassurez-vous, nous allons décomposer chaque concept de manière accessible pour vous faire découvrir comment notre perception sonore est intrinsèquement liée à la logique mathématique de notre cerveau. C’est passionnant, alors oubliez vos a priori. Après tout, tout apprentissage devient plaisant lorsqu’il est bien expliqué.
Au début de nos discussions sur ce site, nous avons souligné que le son est une onde et que sa fréquence détermine la note musicale.
Mais qu’est-ce que la fréquence exactement ? C’est une mesure de répétition dans le temps. Imaginez une roue de vélo qui tourne. Si elle effectue un tour complet en une seconde, sa fréquence est d' »un tour par seconde », soit « un Hertz ».
Le Hertz, simplement le nom donné à l’unité de fréquence, est souvent abrégé en « Hz ». Si, dans notre exemple, la roue effectue 10 tours en une seconde, alors sa fréquence est de 10 Hertz (10 Hz).
Bien, mais quel rapport avec le son ? Le son, également une onde, oscille à certaines fréquences. Si une onde sonore oscille une fois en une seconde, sa fréquence est de 1 Hz. Si elle oscille 10 fois en une seconde, sa fréquence est de 10 Hz. Chaque fréquence correspond à un son distinct (une note différente). Par exemple, la note La correspond à une fréquence de 440 Hz.
Et les mathématiques dans tout ça ? On a observé que lorsqu’une fréquence est doublée, la note reste la même. Par exemple, le La (440 Hz) multiplié par 2 (donnant 880 Hz) est toujours un La, simplement une octave plus haute.
Pour descendre d’une octave, il suffit de diviser la fréquence par deux. On en déduit que la relation entre une note et son octave est de ½.
Les expériences de Pythagore
Avant de poursuivre, faisons un bond dans le passé, en Grèce antique. Un homme nommé Pythagore y a fait des découvertes capitales en mathématiques et en musique. Ce que nous avons mentionné à propos des octaves, il l’a découvert en expérimentant avec une corde tendue.
Imaginez une corde fixée à ses extrémités. Lorsqu’on la fait vibrer (voir l’illustration ci-dessous), elle émet un son.

Pythagore a divisé cette corde en deux, puis a joué chaque moitié. Le son produit était le même, mais plus aigu, car c’était la même note, une octave plus haut.

Il ne s’est pas arrêté là et a essayé de diviser la corde en trois parties.

Il a découvert qu’un nouveau son émergeait, différent du précédent. Ce n’était plus la même note une octave plus haut, mais une note distincte, harmonieuse avec le son original. Ces divisions présentent des rapports mathématiques de 1/2 et 2/3, appréciés par notre cerveau pour leur logique claire.
Il a continué ses expériences, combinant mathématiquement les sons pour créer des échelles qui ont inspiré plus tard la fabrication d’instruments de musique capables de reproduire ces échelles.
L’intervalle de triton, par exemple, provient du rapport 32/45, une relation complexe, perçue par notre cerveau comme instable et tendue.
Avec le temps, les notes ont reçu les noms que nous leur connaissons aujourd’hui.
Il est intéressant de noter que le cerveau humain interprète généralement les sons comme « agréables » lorsque les fractions ont de petits numérateurs et dénominateurs, comme 2/3, 4/5, 8/5, etc. La fraction 32/45 est considérée comme « désagréable ».
Bien que non prouvé scientifiquement, cela pourrait s’expliquer par la combinaison des périodes : des périodes très désalignées sont plus difficiles à interpréter. Par exemple, un son jouant toutes les deux secondes, et un autre toutes les trois secondes (fraction de 2/3), crée un motif rythmique facilement identifiable. En revanche, des sons jouant selon des proportions de 32 sur 45 forment un motif rythmique complexe.
En pratique, comme déjà vu, une note musicale est formée de battements rapides (ex. : 220 battements par seconde = 220 Hz).
Quand on joue deux notes simultanément, on compare un son frappant X fois par seconde à un autre frappant Y fois par seconde, créant une fraction X/Y.
Si cette fraction se simplifie en petits nombres, le motif rythmique est plus facilement interprétable.
Autrement dit, chaque note possède un rythme associé, et le cerveau humain interprète ces rythmes dans une échelle de hauteur. La superposition de deux notes est, en essence, une superposition rythmique. Si le rythme résultant est simple et identifiable, l’interprétation sonore en est plus agréable.
Les Mathématiques des Échelles Musicales

De nombreuses cultures ont élaboré leurs propres échelles musicales, à l’instar du peuple chinois. S’inspirant de l’expérience de Pythagore avec les cordes, ils ont commencé par jouer la note C sur une corde tendue, puis l’ont divisée en trois parties, comme expliqué précédemment.
Le résultat de cette division était la note G. Constater l’harmonie entre ces notes les a conduits à répéter la procédure à partir de G, aboutissant à la note D, en harmonie avec G et C.
En poursuivant avec D, ils ont obtenu A, puis en partant de A, ils sont arrivés à E.
Toutefois, lorsqu’ils ont divisé pour obtenir la note B, le son produit en combinaison avec C (la première note de l’expérience) n’était pas harmonieux. Ces notes, très proches l’une de l’autre, créaient une dissonance.
C’est pourquoi les Chinois ont conclu leur exploration avec C, G, D, A et E, excluant B. Ces notes ont formé la base de la musique chinoise, constituant une échelle pentatonique à cinq notes, emblème de l’harmonie et de la stabilité de la culture orientale.
Depuis sa création, la échelle pentatonique reste un choix privilégié pour les mélodies, comme évoqué dans notre article sur cette échelle. Mais revenons aux notes et fréquences, puisque jusqu’à présent, seules cinq notes de la échelle ont été abordées.
Contrairement à la musique orientale, la musique occidentale, avec ses 12 notes, n’a pas écarté B. Les Occidentaux, remarquant la proximité entre C et B, ont cherché à créer une échelle plus complète, où chaque note serait espacée de façon égale, comme le demi-ton entre C et B. Par conséquent, entre C et D, une note intermédiaire était nécessaire, car l’écart entre ces deux notes (deux demi-tons) était supérieur à celui entre C et B (un demi-ton). Par l’analyse des fréquences, on découvre que multiplier la fréquence de B par 1.0595 donne celle de C:
- Fréquence de B: 246,9 Hz
- Fréquence de C: 261,6 Hz
Ainsi, 246,9 x 1.0595 = 261,6 Hz (note C).
Pour garder cette relation constante entre les notes, nous répétons ce processus pour déterminer la note suivant C. Par exemple, en multipliant la fréquence de C par 1.0595 :
261,6 x 1.0595 = 277,2 Hz (note C dièse)
En continuant cette démarche, on obtient toute la échelle chromatique. Multiplier douze fois la fréquence de C par 1.0595 ramène à C, une octave plus haut. Cela s’explique car 1.0595 est la douzième racine de 2.
Notez que la racine multipliée par elle-même 12 fois est (![]() )12 = 2.
)12 = 2.
Nous savons qu’une note doublée en fréquence donne la même note, une octave plus haute.
Ces chiffres ne sont pas fortuits. L’objectif était de diviser une octave en 12 parties égales, pour que la douzième note soit identique à la première, une octave au-dessus. C’est l’origine de la échelle tempérée, ou chromatique.
Trouver des Notes à partir de Fréquences
Pour mieux comprendre, observons les notes sur un piano :

Si le premier C (à gauche) a une fréquence f, le second C (une octave plus haut) aura une fréquence 2f. Pour atteindre le C suivant, multipliez 2f par 2, obtenant 4f, et ainsi de suite jusqu’au dernier C à 8f. La logique est la suivante :
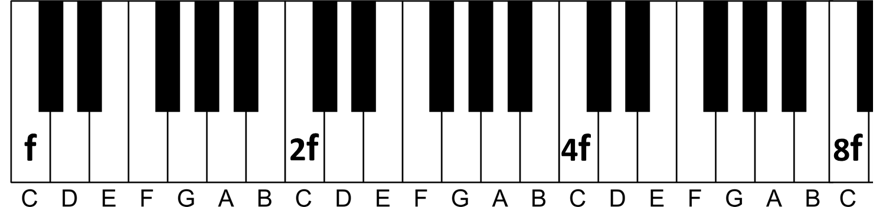
Mais qu’en est-il des fréquences intermédiaires comme 3f, 5f, 6f, 7f ? Examinons cela. Pour la fréquence 3f, se trouvant entre 2f et 4f, on avance de k demi-tons (chaque demi-ton correspondant à environ 1.0595) jusqu’à ce que (1.0595^k)*2f = 3f. On trouve k = 7, car 1.0595^7 ≈ 1.5.
Ainsi, avancer de 7 demi-tons à partir de 2f atteint la note 3f, soit G:
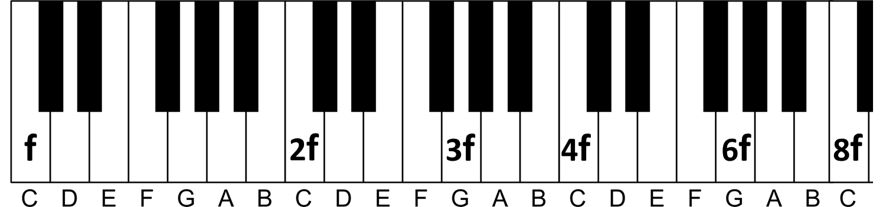
La note 6f, étant une octave au-dessus de 3f (3f*2 = 6f), est identifiée de la même manière.
En appliquant la même méthode, on trouve la note 5f, située entre 4f et 6f :
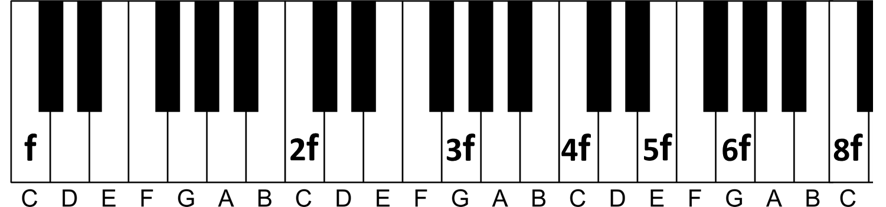
Pour les notes basses, on inverse le processus : on divise par 2. Ainsi, la note E (5f) une octave en dessous sera (5/2)*f, et une autre octave en dessous, (5/4)*f. Il en va de même pour la note 3f :
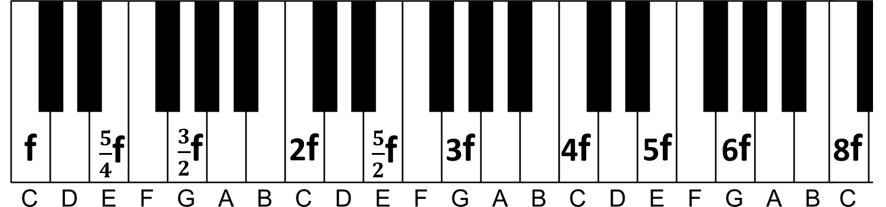
Ainsi, les rapports 5/4 et 3/2 mentionnés au début avec l’expérience de Pythagore se concrétisent sur notre piano.
En utilisant ces techniques, nous pouvons précisément établir toutes les fractions de la première octave :
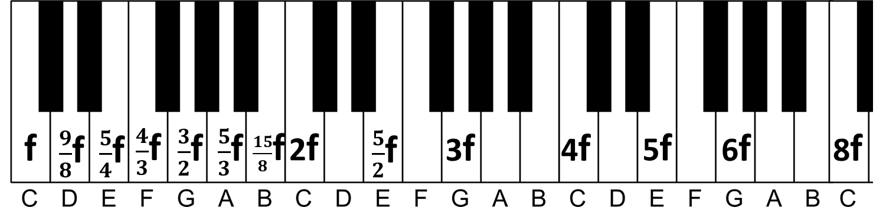
Pour savoir si deux notes jouées ensemble sonnent harmonieusement, il suffit de diviser leurs fréquences et de simplifier la fraction. Un grand dénominateur indique une dissonance.
Exemples :
La quinte parfaite, comme celle entre les notes E et B, est musicalement très plaisante. Peut-on le démontrer mathématiquement ? Prenons l’exemple de la fraction (5/4)/(15/8) qui se simplifie en 2/3, une fraction simple avec de petits dénominateurs, tout comme on s’y attendait.
Et entre B et C ? Ces notes, séparées d’un demi-ton, créent une dissonance auditive. Analysons cela mathématiquement : (15/8) / (2/1) donne 15/16, une fraction complexe, confirmant nos attentes.
Le Logarithme en Musique
Pour ceux qui s’y connaissent en mathématiques, vous avez sans doute remarqué que les calculs de fréquences et de racines font implicitement appel au logarithme en base 2. C’est pourquoi les fabricants de pianos intègrent souvent un graphique logarithmique sur l’instrument, en référence à cette interaction entre mathématiques et musique. Regardez :
Exemple de graphique logarithmique :
Corps de piano :

Explorer Plus Loin
Il existe bien d’autres liens mathématiques dans le domaine musical. Pour les explorer, il faut aborder des concepts plus avancés, comme la série de Fourier. Cette série décrit le comportement d’une onde en physique, en combinant un harmonique principal et plusieurs harmoniques secondaires. Voici comment elle se présente :
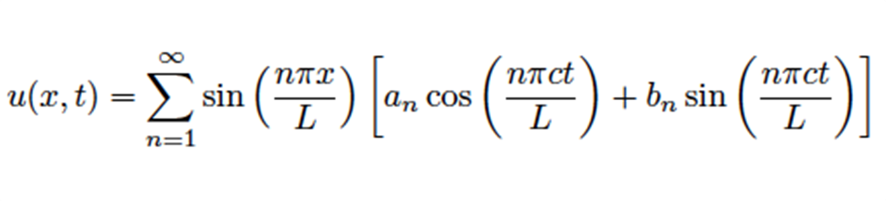
Lorsqu’une corde vibre, le son que nous entendons est une combinaison de multiples fréquences, toutes multiples de la fréquence fondamentale. Cette dernière est la plus dominante, tandis que les autres, appelées harmoniques, enrichissent le son.
La diversité des harmoniques confère au son sa richesse et sa texture. Un diapason, par exemple, produit un son avec peu d’harmoniques, principalement la fréquence fondamentale. C’est idéal pour accorder des instruments, mais son timbre est relativement pauvre.
Chaque instrument possède un timbre unique, déterminé par la manière dont les harmoniques se superposent à la fréquence fondamentale. L’harmonica et la flûte, par exemple, sonnent différemment pour cette raison.
De plus, différents matériaux influencent les harmoniques produites. Ainsi, la qualité d’un instrument tient compte des propriétés de chaque matériau, comme le type de bois d’une guitare.
En amplifiant un instrument, chaque composant du circuit peut affecter les harmoniques, altérant la qualité sonore. D’où l’importance d’investir dans de bons équipements.
Enfin, l’ingénierie sonore, qui développe des dispositifs pour capturer et stocker numériquement les ondes sonores, vise à préserver la forme d’onde originale. Le traitement en studio, comme la réduction de bruit, s’appuie aussi sur ces principes, cherchant à éliminer les harmoniques indésirables.
Réflexions Finales
Notre but était de vous expliquer le fonctionnement mathématique de la musique et la manière dont notre cerveau perçoit ces relations logiques.
Il est important de noter que nos explications reposent sur des approximations (chiffres arrondis), car une analyse plus détaillée serait trop complexe pour la plupart des lecteurs et nécessiterait des tests mathématiques et physiques plus approfondis.
Il n’est pas indispensable de retenir tous les détails abordés ici. Retenez simplement que la musique n’émerge pas du néant ; elle est le fruit d’une structuration numérique, interprétée par notre cerveau.
En réalité, si vous êtes musicien, vous êtes aussi, d’une certaine manière, mathématicien. Les sensations de plaisir que vous éprouvez en écoutant de la musique sont en fait le résultat de calculs subtils effectués par votre cerveau.
Votre cerveau adore faire des calculs ; c’est une véritable machine à calculer ! Plus vous vous entraînez, étudiez et comprenez la musique, plus cette aptitude se développe. Vous commencerez même à apprécier des musiques qui, auparavant, ne vous procuraient pas de grandes émotions.
Prenons l’exemple d’un étudiant en première année de physique. Si celui-ci lit un livre de physique moderne, il lui semblera incompréhensible, sans intérêt. Mais quelques années plus tard, après avoir acquis de solides bases en mathématiques, ce même livre pourrait éveiller en lui une passion pour la physique et même devenir sa vocation.
Continuez vers : Module 12
Revenez à : Demystifiant La Musique
