Dans l’article précédent sur les intervalles augmentés, diminués et parfaits, nous avions limité l’utilisation des termes « augmenté » et « diminué » aux 4ème et 5ème degrés. Cependant, nous allons maintenant voir comment ces termes s’appliquent également aux autres degrés.
Pour les degrés qui portent déjà la dénomination « majeur » et « mineur », le terme « augmenté » désigne un demi-ton au-dessus du degré majeur. Voici quelques exemples :
- Le deuxième degré majeur est à deux demi-tons de la tonique. Le deuxième degré augmenté est alors à trois demi-tons de la tonique.
- Le troisième degré majeur est à quatre demi-tons de la tonique. Le troisième degré augmenté se trouve à cinq demi-tons de la tonique.
De même, le terme « diminué » signifie un demi-ton en dessous du degré « mineur ». Par exemple :
- Le troisième degré mineur est à trois demi-tons de la tonique. Le troisième degré diminué est alors à deux demi-tons de la tonique.
- Le septième degré mineur est à dix demi-tons de la tonique. Le septième degré diminué se trouve à neuf demi-tons de la tonique.
Faisons un récapitulatif de tout ce que nous avons appris sur les degrés pour plus de clarté.
Si vous rencontrez encore des difficultés à penser en termes de tons et de demi-tons, référez-vous au diagramme suivant (où DT signifie « demi-ton ») :
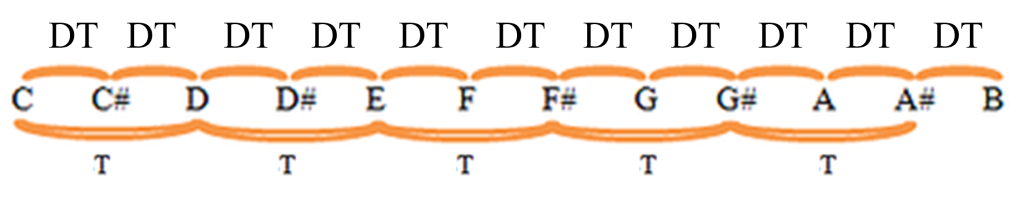
Pour tous les degrés, nous aurons les distances suivantes :
En utilisant l’exemple de C comme premier degré :
- Seconde Majeure – c’est 1 ton de la tonique (D)
- Seconde Mineure – c’est un demi-ton de la tonique (Db)
- Seconde Augmentée – c’est 1 ton et demi de la tonique (D#)
- Seconde Diminuée – N’existe pas
Observation : Nous avons choisi d’écrire les altérations liées à D ici parce que c’est la note du deuxième degré par rapport à C. Nous aurions pu écrire, par exemple, Eb au lieu de D#, mais l’idée ici est de penser en D.
- Troisième Majeure – c’est 2 tons de la tonique (E)
- Troisième Mineure – c’est 1 ton et demi de la tonique (Eb)
- Troisième Augmentée – c’est 2 tons et demi de la tonique (E#)
- Troisième Diminuée – c’est 1 ton de la tonique (Ebb)
Observation : Juste pour souligner, nous avons mis ici toutes les altérations liées à E, car c’est le troisième degré de C. C’est pour cela que Ebb apparaît au lieu de D. Ainsi, la logique est plus claire. Nous continuerons à suivre cette induction.
Autres intervalles musicaux
- Quarte Parfaite – est à 5 demi-tons de la tonique (F)
- Quarte Augmentée – est à 6 demi-tons de la tonique (F#)
- Quarte Diminuée – est à 4 demi-tons de la tonique (Fb)
- Quinte Parfaite – est à 7 demi-tons de la tonique (G)
- Quinte Augmentée – est à 8 demi-tons de la tonique (G#)
- Quinte Diminuée – est à 6 demi-tons de la tonique (Gb)
- Sixième Majeure – est à 9 demi-tons de la tonique (A)
- Sixième Mineure – est à 8 demi-tons de la tonique (Ab)
- Sixième Augmentée – est à 10 demi-tons de la tonique (A#)
- Sixième Diminuée – est à 7 demi-tons de la tonique (Abb)
- Septième Majeure – est à 11 demi-tons de la tonique (B)
- Septième Mineure – est à 10 demi-tons de la tonique (Bb)
- Septième Augmentée – est à 12 demi-tons de la tonique (B#)
- Septième Diminuée – est à 9 demi-tons de la tonique (Bbb)
Cette définition peut sembler un peu inutile, après tout, le deuxième degré augmenté est identique au troisième degré mineur, par exemple. Cela semble être quelque chose créé juste pour nous embrouiller. Eh bien, il n’est vraiment pas nécessaire d’utiliser cette nomenclature « augmentée » et « diminuée » pour les degrés qui ont déjà la définition « majeur » et « mineur ». Cependant, cela peut nous aider.
Attendez une minute, aider ?!
C’est exact. Supposons que nous voulions construire un accord qui a une certaine triade. Construisons cette triade avec la quinte diminuée au lieu de la quinte parfaite, d’accord ? Disons, do mineur avec quinte diminuée. Puisque l’accord est mineur, nous savons déjà que le troisième degré est mineur :
- Premier degré : C
- Troisième degré mineur : Eb
- Quinte diminuée : Gb
C’est notre C mineur avec quinte diminuée. Disons que maintenant le chanteur du groupe nous demande d’ajouter la note la à cet accord. D’accord, nous avons ajouté la note la, mais comment allons-nous appeler cet accord ?
La note la est le sixième degré majeur, donc l’accord sera appelé : « C mineur avec quinte diminuée et sixième majeure ».
Ok, jusqu’ici nous n’avons pas appliqué de nouveaux concepts. Cet accord a seulement 4 notes et a un nom très long et compliqué. Les tétrades les plus courantes que nous connaissons ont des noms simples (B mineur septième, F majeur septième, etc.), mais notre Cm6(b5) est ennuyeux à visualiser à cause du nom.
Alors appliquons les concepts que nous venons d’apprendre. Le sixième degré majeur peut aussi être appelé un septième degré diminué.
C’est intéressant à observer, car notre tétrade ici aurait les degrés de base 1, 3, 5 et 7 (qui est plus courant et plus facile à visualiser que 1, 3, 5 et 6).
Super, mais cela a-t-il simplifié notre nomenclature ? Oui ! Puisque nous avons une tétrade commune (degrés 1, 3, 5 et 7) et que deux de ces degrés sont diminués (le cinquième et le septième), il a été décidé que cet accord serait appelé un « accord diminué« . C’est-à-dire, au lieu de « C mineur avec quinte diminuée et sixième majeure », nous avons « C diminué » (également appelé Cdim, ou Cº).
C’était juste une application pour cette terminologie. Il existe d’autres situations dans lesquelles vous verrez ces concepts aussi, lorsque nous voulons garder l’accent sur certaines notes dans certains contextes, il est donc bon pour vous de connaître cette nomenclature pour ne pas être effrayé lorsque vous voyez « troisième degré augmenté », par exemple. Ce n’est qu’une question de référence.
Vous n’avez pas non plus à vous soucier des notations d’accords que nous venons de montrer, car dans les prochains articles, nous vous apprendrons en détail comment former des accords et écrire leurs notations d’accords respectives.
Revenir au : Module 2
Poursuivre vers : Module 3
